Blog/2025-07-09/It's Just Thresholds: Difference between revisions
Created page with "thumb|Non-uniformity is all we were looking for but this nice peak is even better A lot of things that appear to have hit some step function in growth or decline are really just artifacts of thresholds. I think a typical example of this is the classification of overweight, obese, and extremely obese. These are thresholds on the BMI - which is not uniformly distributed. The most common way of reporting all of this is in "percentage..." |
mNo edit summary |
||
| Line 5: | Line 5: | ||
This is just an artifact of the tools you're using to measure everything. It doesn't mean that "something happened in 1970" for the curve to have accelerated upwards. Even if we maintained the same upward increase in calories at a constant pace (say because we simply got richer) there would be a moment when the curve inflected upwards, not because of seed oils or microplastics or anything of the sort but simply because of the fact that the underlying distribution started out non-uniform. | This is just an artifact of the tools you're using to measure everything. It doesn't mean that "something happened in 1970" for the curve to have accelerated upwards. Even if we maintained the same upward increase in calories at a constant pace (say because we simply got richer) there would be a moment when the curve inflected upwards, not because of seed oils or microplastics or anything of the sort but simply because of the fact that the underlying distribution started out non-uniform. | ||
I made this little toy with Claude to illustrate the concept. It shows a normal distribution about 100 with a standard deviation of 16. Suppose we called people who were above 148 (3x the standard deviation) Supers. To start with, a mere 0.13% of the population are Supers. Let's say that we want people to be more super and we've figured out that giving them one kg of rice a year moves them up on this index by 1. After a year, we'll see that the mean is now 101 on our original scale and 0.17% of them are Supers by the original scale. | I made this little toy with Claude to illustrate the concept. | ||
{{#visualization:normal-threshold|1000|1200}} | |||
It shows a normal distribution about 100 with a standard deviation of 16. Suppose we called people who were above 148 (3x the standard deviation) Supers. To start with, a mere 0.13% of the population are Supers. Let's say that we want people to be more super and we've figured out that giving them one kg of rice a year moves them up on this index by 1. After a year, we'll see that the mean is now 101 on our original scale and 0.17% of them are Supers by the original scale. | |||
[[File:Percentage of Population vs. Threshold.png|thumb]] | [[File:Percentage of Population vs. Threshold.png|thumb]] | ||
| Line 11: | Line 15: | ||
No, it's just that we had a fixed threshold on a fixed scale, and a non-uniform distribution that is being moved to the right. Consequently, the upper threshold we applied grows like the cumulative distribution function of the probability distribution function of the population. And for a non-uniform latter it should be unsurprising there is a non-uniform former. | No, it's just that we had a fixed threshold on a fixed scale, and a non-uniform distribution that is being moved to the right. Consequently, the upper threshold we applied grows like the cumulative distribution function of the probability distribution function of the population. And for a non-uniform latter it should be unsurprising there is a non-uniform former. | ||
[[Category:Blog]] | [[Category:Blog]] | ||
Revision as of 03:08, 10 July 2025
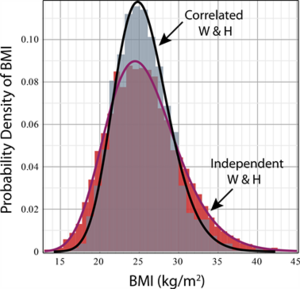
A lot of things that appear to have hit some step function in growth or decline are really just artifacts of thresholds. I think a typical example of this is the classification of overweight, obese, and extremely obese. These are thresholds on the BMI - which is not uniformly distributed. The most common way of reporting all of this is in "percentage of the population that is in category A". But the underlying distribution of weight is most affected by calories/time. If you gave everyone +x calories/time, you would shift the BMI curve to the right by some amount. But your "percentage in category A" would vary in a non-linear manner.
This is just an artifact of the tools you're using to measure everything. It doesn't mean that "something happened in 1970" for the curve to have accelerated upwards. Even if we maintained the same upward increase in calories at a constant pace (say because we simply got richer) there would be a moment when the curve inflected upwards, not because of seed oils or microplastics or anything of the sort but simply because of the fact that the underlying distribution started out non-uniform.
I made this little toy with Claude to illustrate the concept.
Visualization for ▼ normal-threshold
It shows a normal distribution about 100 with a standard deviation of 16. Suppose we called people who were above 148 (3x the standard deviation) Supers. To start with, a mere 0.13% of the population are Supers. Let's say that we want people to be more super and we've figured out that giving them one kg of rice a year moves them up on this index by 1. After a year, we'll see that the mean is now 101 on our original scale and 0.17% of them are Supers by the original scale.
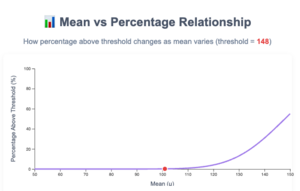
All right, so one kg of rice makes 0.04% of our population into Supers every year. But does it? By the time the mean is at 110 on the original scale, going to 111 makes an additional 0.16% of our population into Supers. The curve starts inflecting up. Everyone panics. What did we change in year 10? Did we start giving everyone like 4 times as much rice or something? Was it seed oils? Was it microplastics? Was it 5G?
No, it's just that we had a fixed threshold on a fixed scale, and a non-uniform distribution that is being moved to the right. Consequently, the upper threshold we applied grows like the cumulative distribution function of the probability distribution function of the population. And for a non-uniform latter it should be unsurprising there is a non-uniform former.
